Dauermagnete haben für viele Leute etwas Geheimnisvolles an sich…
«Wozu braucht man denn Dauermagnete?» ist deshalb eine viel gehörte Frage. Nur wenige wissen, dass Dauermagnete ein nicht mehr wegzudenkender Teil der modernen Technik sind, dabei benützen wir alle tagtäglich deren Dienste. Der Kopfhörer oder Lautsprecher, das Smartphone, der Elektroantrieb im EL-Automobil, EL-Fahrrad, EL-Trottinett, EL-Rollstuhl, Windräder zur Stromerzeugung sind nur einige davon. In der Technik werden Dauermagnete eingesetzt in Messgeräten elektrischer und mechanischer Grössen, als akustische Wandler, als elektromechanische Wandler, als Maschinenelemente und man bedient sich der magnetischen Kraftwirkung.
Auch in der Medizin, der Biologie und in der Kernphysik sind Dauermagnete heute unentbehrlich. Durch die weite Verbreitung und den sehr günstigen Preis, vornehmlich der Neodym-Magnete, auch Supermagnete genannt, finden diese eine weite Verbreitung in Spiel und Spass.
Trotz dieser vielseitigen Anwendungen besitzt nur eine relativ kleine Zahl von Technikern fundierte Kenntnisse über die Theorie und Anwendung der Dauermagnete. Das mag wohl daher kommen, dass leider nur wenige Hoch- und Fachschulen das Wissen und die Erkenntnisse über die Eigenschaften der Dauermagnete vermitteln.
Magnetische Grundbegriffe
1. Magnetischer Fluss
Das magnetische Feld um einen magnetisierten Dauermagneten hat man sich als einen Raum vorzustellen, der mit magnetischen Kraftlinien ausgefüllt ist. Die Kraftlinien treten am Nordpol des Magneten aus und laufen in grossem Bogen durch den Raum zum Südpol. Jede Kraftlinie bildet so einen eigenen Kreis.
Der magnetische Fluss ist die Gesamtheit aller Kraftlinien.
Das Symbol für den magnetischen Fluss ist Φ (phi) und steht für die gesamte Anzahl Kraftlinien eines Magnetes.
Die Einheit des magnetischen Flusses ist:
1 Maxwell = 1 Kraftlinie
Φ = B ∗ Fm
Gesamt-Magnetfluss = Remanenz in Gauss × Fläche (Querschnitt) Magnet in cm2
2. Remanenz
Je stärker die magnetische Wirkung eines Magnetfeldes an einem bestimmten Ort ist, umso dichter hat man sich dort den Verlauf der Kraftlinien vorzustellen.
Die Remanenz oder Induktion ist die Dichte der Kraftlinien.
Das Symbol der Remanenz ist B und steht für die Anzahl der senkrecht durch eine Fläche von 1 cm2 gehenden Kraftlinien.
Die Einheit der Remanenz oder Induktion ist:
1 Gauss = 1 Kraftlinie pro cm2 = 10-8 Voltsekunden/cm2
Remanenz = (Gesamter magnetischer Fluss in Maxwell)÷(Fläche in cm2, durch die der Magnetfluss austritt)
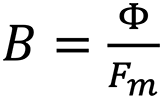
3. Koerzitivkraft
Die Koerzitivkraft hat man sich als die Widerstandsfähigkeit gegen die Entmagnetisierung durch ein äusseres Magnetfeld vorzustellen. Sie ist das einem entmagnetisierenden Einfluss entgegenstehende Haltbarkeitsvermögen der Dauermagnete.
Das Symbol für die Koerzitivkraft ist das Zeichen Hc und steht für die Grösse eines einem Dauermagneten entgegengesetzten äusseren Feldes, welches in der Lage ist, die Remanenz des Dauermagnetes auf null hinunterzudrücken.
Die Einheit der Koerzitivkraft ist:
1 Oersted ≅ 0,8 AW/cm (Amperewindungen pro cm)
4. Magnetomotorische Kraft
Im Inneren jedes Dauermagnetes ist nach seiner Aufmagnetisierung eine magnetische Spannung vorhanden, welche als die Ursache dafür betrachtet werden kann, dass ein Magnetfeld im Raum um den Magnet herum entsteht.
Die magnetomotorische Kraft (MMK) ist die gesamte magnetische Spannung oder die gesamte magnetische treibende Kraft eines Dauermagnetes, welche bewirkt, dass der Raum um den Magnet herum mit Kraftlinien ausgefüllt wird.
Das Symbol der magnetomotorischen Kraft ist Θ (theta) und steht für die gesamte vorhandene magnetische Spannung.
Die Einheit der magnetomotorischen Kraft ist:
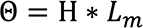
1 Gilbert = 1 Oersted × cm ≅ 0,8 Amperewindungen
Magnetomotorische Kraft = Koerzitivfeldstärke ∗ Länge des Magnetes in cm
5. Koerzitivfeldstärke
Je weiter in den Raum hinaus die Kraftlinien eines Magnetfeldes getrieben werden, umso grösser hat man sich die magnetische Feldstärke vorzustellen.
Die Koerzitivfeldstärke ist die magnetische Spannung pro Längeneinheit eines magnetischen Feldes.
Das Symbol der Koerzitivfeldstärke ist H und steht für die magnetische Spannung oder magnetomotorische Kraft, die in 1 cm Länge eines Dauermagnetes enthalten ist.
Die Einheit der Koerzitivfeldstärke ist:
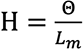
1 Oersted ~ 0,8 AW/cm (Amperewindungen pro cm)
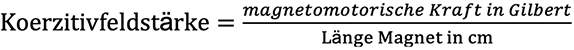
Die Verknüpfung mit der in der Elektrizitätslehre üblichen Grösse der Amperewindung entsteht wie folgt:
Die magnetische Spannung einer von elektrischem Strom durchflossenen Spule wird der magnetischen Spannung eines Dauermagnetes gleichgesetzt. Die magnetische Spannung einer Spule oder deren Durchflutung berechnet sich nach der Formel I ∗ n / L = AW/cm, wobei I dem fliessenden Strom in Ampere, n der Anzahl Windungen des Drahtes und L der Länge der Spule in cm entsprechen, woraus das Produkt Amperewindungen/cm resultiert.
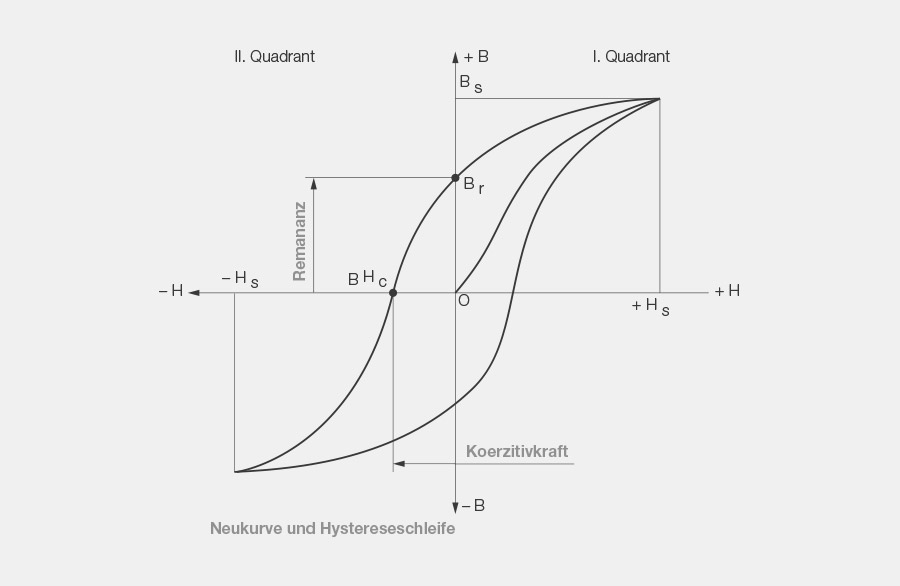
6. Hystereseschleife
Die Hystereseschleife ist die grafische Darstellung des Verhaltens eines Materials in einem äusseren Magnetfeld. Zu diesem Zweck wird in einem rechtwinkligen Koordinatensystem die Remanenz B auf der Ordinate und die KoerzitivFeldstärke H auf der Abszisse eingetragen. Nun wird das Material, von dem die Hystereseschleife zu ermitteln ist, einem allmählich wachsenden Magnetfeld ausgesetzt. Dadurch steigt die Remanenz im Prüfling an. Trägt man diesen Anstieg im ersten Quadranten des Koordinatensystems ein, so erhält man die sogenannte Neukurve, welche bei + HS(Sättigungsfeldstärke) einen für jeden ferromagnetischen Werkstoff typischen Sättigungswert erreicht. Diese Sättigung wird auch maximale Induktion genannt.
Lässt man nun die Feldstärke des äusseren Magnetfeldes abnehmen, so geht die Remanenz in dauermagnetischen Materialien nicht auf der Neukurve zurück. Die lnduktionswerte liegen höher und es verbleibt bei vollständig abgeschaltetem äusserem Magnetfeld (H = 0) ein endlicher Wert Br zurück. Dies ist die remanente Induktion oder der Restmagnetismus im Remanenzpunkt.
Wird nun das äussere Feld umgepolt und lässt man es so ansteigen, so nimmt die Remanenz B weiter ab, um im sogenannten Koerzitivpunkt BHc ganz zu verschwinden (B = 0).
Moderne Materialien aus der Gruppe der Seltenen Erden bilden eine tiefere Verankerung der magnetischen Dipole und werden erst bei einem zum Teil mehrfach höheren äusseren Magnetfeld umgepolt. JHc. Dieser Wert ist entscheidend für eine Zähigkeit im Ummagnetisieren von Magnetwerkstoffen in starken Gegenfeldern und Temperaturbeständigkeit in z. B. Elektromotoren. Zum Berechnen von magnetischen Kreisen wird der Wert BHc verwendet.
Mit dem weiteren Verstärken des Magnetfeldes läuft B, jetzt mit umgekehrtem Vorzeichen, auf einem negativen Ast zu einem dem ersten entgegengesetzten Sättigungspunkt. Wiederholt man nun das Ganze mit nochmals geänderter Polarität, so läuft B auf einer zur ersten Kurve symmetrischen Bahn wieder zum ersten Sättigungspunkt zurück. Die so geschlossene Schleife nennt man die Hystereseschleife. Die Fläche, die sie einschliesst, stellt die beim Ummagnetisieren in Wärme umgesetzte Energie dar.
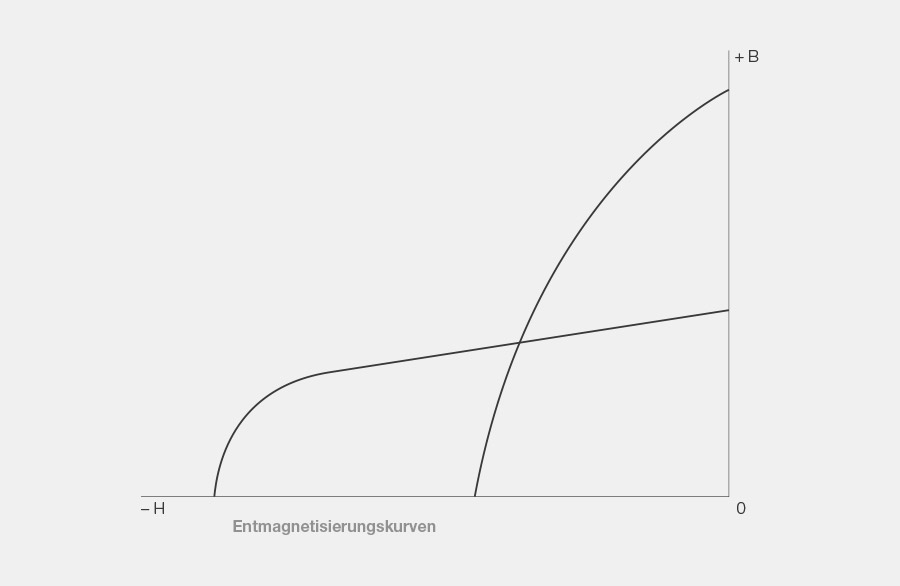
7. Entmagnetisierungskurve
Diese für Dauermagnete ausserordentlich wichtige Kennlinie ist ein Ausschnitt aus der Hystereseschleife. Sie zeigt den Verlauf von B im zweiten Quadranten bei einer der Magnetisierung entgegengesetzten, ansteigenden Feldstärke. Sie ist ein Kriterium für die Güte eines Magnetwerkstoffes und für die Berechnung von Dauermagneten äusserst wichtig.
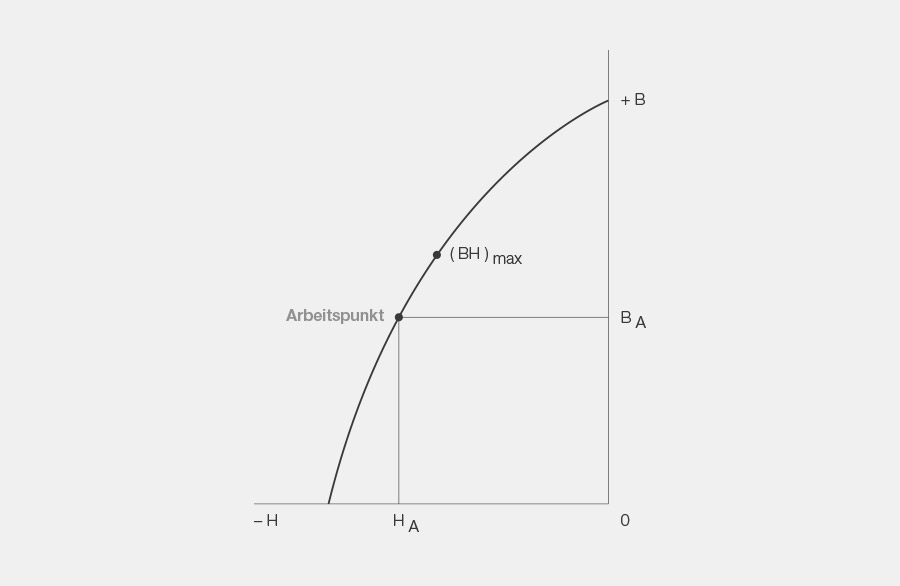
8. Arbeitspunkt
Der Mechanismus, wie sich der Arbeitspunkt eines Magnetes von selbst einstellt, ist recht kompliziert. Für die Praxis genügt folgende qualitative Erklärung:
Die Lage des Arbeitspunktes eines Magnets, der in einem Joch oder in einer Solenoidspule aufmagnetisiert wurde, liegt nach dem Abschalten des durch Strom erzeugten äusseren magnetischen Feldes im Remanenzpunkt Br. Durch das Öffnen des Joches oder nach dem Magnetisierpuls entsteht nun ein Luftspalt im bis jetzt vollständig geschlossen gewesenen Magnetkreis. An den Flächen des Luftspaltes bilden sich magnetische Pole. Diese Pole „magnetisieren“ den Luftspalt, d. h., sie geben einen magnetischen Fluss ab und bauen im Luftspalt ein magnetisches Feld auf. Gleichzeitig entmagnetisiert sich der Magnet so weit als notwendig, um das Magnetfeld aufzubauen, und zwar je nach Länge des Luftmagneten.
Die zum Feldaufbau notwendige magnetomotorische Kraft wird durch die mechanische Energie erzeugt, die notwendig ist, um den Magnetkreis zu öffnen, oder um den Magnet aus dem Joch herauszuziehen. Diese magnetomotorische Kraft bewirkt, dass der Magnet sich selbst entmagnetisiert, da sie der Magnetisierung entgegengesetzt gerichtet ist. Deshalb wandert die Remanenz B vom Induktionspunkt Br auf der Entmagnetisierungskurve in Richtung H zu einem neuen Punkt BA, dem Arbeitspunkt, dessen Lage davon abhängig ist, wie weit der Magnetkreis geöffnet wurde und wie gross die Koerzitivkraft des Magnetmaterials ist. Seine Lage lässt sich beeinflussen, indem der Magnet entsprechend der Koerzitivkraft länger oder kürzer gewählt wird.
Der Arbeitspunkt eines Magnetes auf der Entmagnetisierungskurve zeigt dessen momentanen magnetischen Zustand an. Dem Arbeitspunkt zugehörig sind der remanente Arbeitspunkt BA und der koerzitive Arbeitspunkt HA.
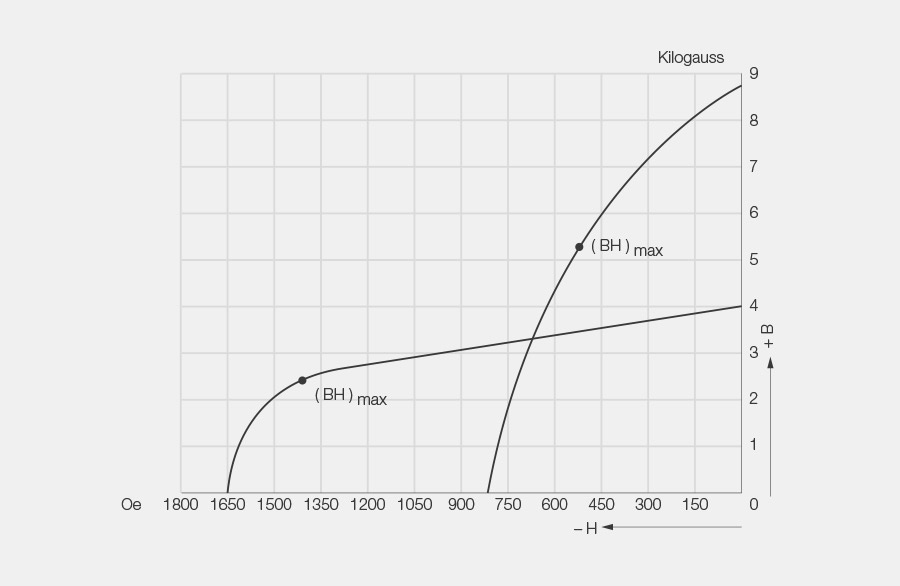
9. (BH)max-Punkt
Der (BH)max-Punkt liegt an der Stelle der Entmagnetisierungskurve, wo die einander zugehörigen Werte der Remanenz und der Koerzitivkraft miteinander multipliziert das grösste Produkt ergeben.
10. Energieprodukt
Dieses Produkt errechnet sich aus den einander zugehörigen Werten der Remanenz und der Koerzitivfeldstärke, die auf der Entmagnetisierungskurve abgelesen werden können. Es zeigt die remanente Energie eines Magnetwerkstoffes an.
Um einen Magnetwerkstoff richtig auszunutzen, ist es zweckmässig, den magnetischen Kreis so auszulegen, dass der Magnet im (BH)max-Punkt arbeitet, weil damit die grösstmögliche Energie im Luftspalt für ein gegebenes Volumen von Magnetwerkstoff zur Verfügung steht.
Das (BH)max-Produkt gibt das grösstmögliche Arbeitsvermögen eines Magnetmateriales bezogen auf die Raumeinheit an.
Das Symbol des Energieproduktes ist (BH)max und steht für das grösstmögliche Produkt (BA ∗ HA) eines Magnetmateriales.
11. Streufluss
Die meisten Dauermagnete arbeiten aber nicht auf ihrer ganzen Länge im selben Arbeitspunkt. Nur in der neutralen Zone (auf halbem Weg zwischen den beiden Polen) geht der gesamte Magnetfluss durch den Magnet. Dieser gesamte Magnetfluss setzt sich aus dem Nutzfluss in einem Luftspalt und dem unvermeidlichen Streufluss zusammen. Will man einen Magnet auf seiner ganzen Länge im selben Arbeitspunkt arbeiten Iassen, so muss dieser Magnet gegen die Mitte dicker werden, um dem Streufluss entgegenzuwirken. Dies ist ein Grund, weshalb bei vielen Hufeisenmagneten die Schenkel konisch ausgebildet sind.
Im praktischen Gebrauch nimmt man aber an, dass die Magnete auf ihrer ganzen Länge im selben Arbeitspunkt arbeiten, d. h. überall denselben Magnetfluss aufweisen. In den meisten Fällen ist dies genau genug, verlangt aber, dass der Streuverlust in allen Berechnungen, Konstruktionen und Messungen berücksichtigt wird.
12. Reluktanz
Die Reluktanz ist der magnetische Widerstand eines Magnetkreises. Sie ist die Resultierende aller magnetischen Teilwiderstände der verschiedenen Stücke, aus denen der Magnetkreis zusammengesetzt ist. Gebraucht wird der Wert der Reluktanz, um den Magnetfluss zu bestimmen, der in einem bestimmten Teil eines Magnetkreises, z. B. einem Luftspalt, erforderlich ist. Das Symbol für die Reluktanz ist R.
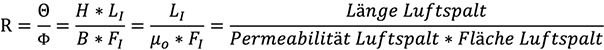
13. Berechnung von Dauermagneten
Bei der Berechnung von Dauermagneten wird am besten von der spezifischen Reluktanz oder deren reziproken Grösse, der spezifischen Permeanz, ausgegangen. Das Schwierigste bei der Ermittlung der spezifischen Reluktanz oder Permeanz ist das Errechnen der Streu- und Potenzialverluste. Wohl gibt es Formeln für die am häufigsten vorkommenden Magnetkreise, mit denen diese Verluste errechnet werden können, aber entweder sind diese Formeln viel zu kompliziert oder die Berechnungen mit vereinfachten Formeln ergeben nur angenäherte Werte. Es ist deshalb sinnlos, einen magnetischen Kreis auf 5 Stellen nach dem Komma genau berechnen zu wollen, wenn dann nur angenähert berechnete Faktoren des Streu- und des Potenzialverlustes zur Verfügung stehen. Auch bei einer vermeintlich exakten Berechnung dieser Faktoren ist es unumgänglich, die Berechnungen durch Messungen an einem Modell nachzuprüfen.
Allgemein kann gesagt werden, dass der Streuverlustfaktor ρ1 (rho1) in den allermeisten Fällen zwischen 2 und 10 liegt. Mit diesem Wert ist der gegebene Querschnitt des Nutzluftspaltes zu multiplizieren, um die unvermeidlichen Streuverluste jedes magnetischen Kreises zu kompensieren. Der Potenzialverlustfaktor ρ2 (rho2) ist viel kleiner und liegt meistens zwischen 1,1 und 1,5. Mit diesem Faktor ist die Länge des gegebenen Nutzluftspaltes zu multiplizieren, um die durch Umbiegen der Kraftlinien und die an den Fugen des Magnetkreises auftretenden Verluste an magnetomotorischer Kraft (MMK) zu kompensieren.
Der Streuverlustfaktor wird in der modernen Literatur als σ (sigma) bezeichnet und der Potenzialverlustfaktor als τ (tau).
Man unterscheidet σr von σ. Der praktische Streufaktor ist σr = Φi ÷ Φen. Der totale Streufaktor ist σ = Φi ÷ Φe. Hierzu sind Φen der Nettofluss im Luftspalt, Φi der Fluss in den Magneten und Φe der gesamte Fluss, der den Luftspalt durchquert.
Da die Ermittlung der genauen Verlustfaktoren so schwierig ist, sollten dauermagnetische Kreise nicht nur aufgrund errechneter Werte konstruiert werden. Erfahrungswerte und Messergebnisse an Versuchsmodellen müssen ebenso berücksichtigt werden. Die Konstruktion dauermagnetischer Kreise ist infolge dieser Schwierigkeiten nicht nur eine rein mathematische Aufgabe, sondern ebenso sehr eine Kunst, die wie übrigens alle Künste Begabung und Erfahrung voraussetzen.
Moderne EDV-gestützte Berechnungsprogramme können sehr zuverlässig im Aufbau definierte Dauermagnetsysteme berechnen. Schwieriger wird es bereits bei Systemen, welche mit mehrpoligen Magneten oder aus mehreren verschiedenpoligen Magneten aufgebaut sind.
Die Berechnungsprogramme können den grundlegenden Aufbau und die Konstruktion eines Magnetsystems noch nicht vorschlagen. Nach wie vor ist das auf einen bestimmten Zweck oder Eigenschaften vorgesehene Magnetsystem zu konstruieren.
Warum so viele Magnetlegierungen?
Die vielen Nuancen von isotropen, anisotropen und kristallorientierten Magnetmaterialien wären sicher nicht hergestellt worden, wenn nicht ein Bedürfnis dafür bestünde. Ein Magnet darf z. B. nur ein absolutes Minimum an Volumen aufweisen, oder er muss Magnetfluss durch einen grossen Luftspalt treiben, oder er muss hohen Temperaturen widerstehen, oder er darf nur sehr wenig kosten, oder er muss vielpolig auf dem Umfang magnetisiert werden können, oder er hat entmagnetisierenden Feldern zu widerstehen. Allen diesen Wünschen kann nur durch ein auf den Verwendungszweck abgestimmtes Magnetmaterial entsprochen werden.
Magnetische Formeln
1. BIOT-SAVARTsches Gesetz
Ein stromdurchflossener Leiter erzeugt ein magnetisches Feld in jedem beliebigen Punkt P ausserhalb des Stromfadens. In Integralform gilt für einen unendlich langen gestreckten Leiter:
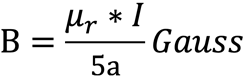
I = Strom in Ampere, a = Abstand vom Punkt P zum Leiter in cm, μr = relative Permeabilität
2. LAPLACEsches Gesetz
Ein stromdurchflossener Leiter der Länge L im Feld anderer stromdurchflossener Leiter oder Permanentmagnete erfährt eine Kraft F. Es gilt:
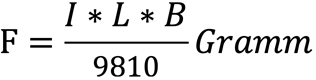
I = Strom in Ampere, L in cm, B = Induktion in Gauss
Gültig für B senkrecht zu L, wobei F wiederum senkrecht zu L und zu B ist. Dabei gilt die Regel der linken Hand: B in Richtung vom Zeigefinger, Stromrichtung entspricht dem Mittelfinger, die Kraft dem Daumen.
3. KIRCHHOFFsche Regeln
In jedem Punkt eines Magnetkreises ist die Summe der ankommenden Flüsse ∑Φe gleich der Summe der abfliessenden Flüsse ∑Φa
In einem in sich geschlossenen Magnetsystem ist die Summe der magnetischen Teilspannungen (Teilspannung=Φ x R, d. h. Fluss mal Reluktanz) gleich der Summe der im System wirksamen magnetomotorischen Kräfte.
Diese Regeln werden manchmal bei magnetischen Kreisen auch Houston’sche Regeln genannt.
4. Formel der Reluktanz
Ein prismatisches Gebilde von Länge L und Querschnitt S hat einen magnetischen Widerstand oder Reluktanz R.
Es gilt:

5. Formel von R. K. Tenzer
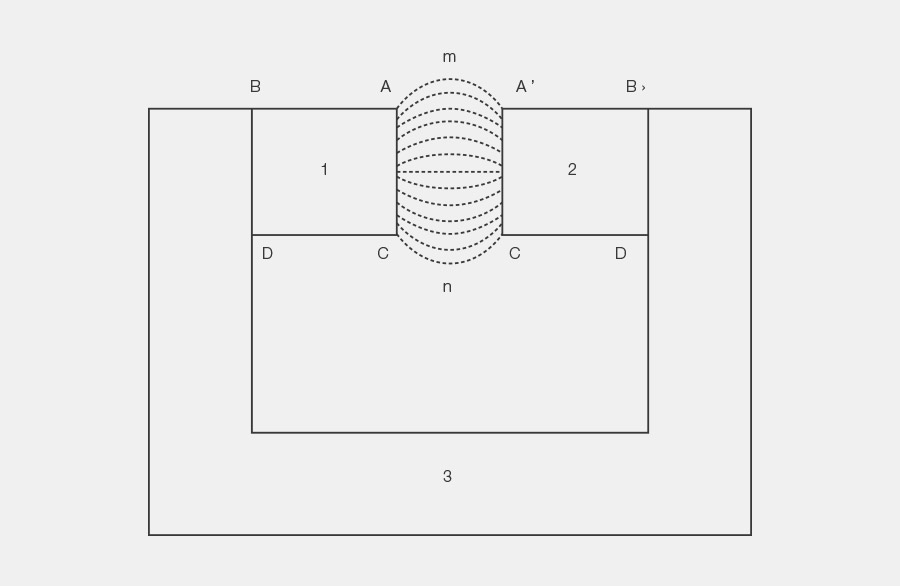
Der praktische Streufaktor eines Dauermagnetkreises nach dem Bild «Symmetrisches Magnetsystem» ist näherungsweise durch folgende Formel gegeben:
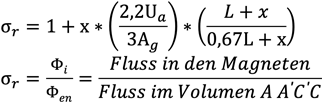
6. Differenzialgleichung von C. Schick
Für den totalen Streufaktor σ eines idealen Dauermagnetkreises nach dem Bild «Symmetrisches Magnetsystem» gilt folgende Differenzialgleichung:
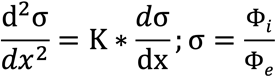
x=Länge vom Luftspalt, K=Konstante
Φe=Fluss im Volumen A m A^‘ C^‘ n C
Φi=Fluss in den Magneten
7. Formeln von C. Schick
Es gelten folgende Beziehungen für den totalen Streufaktor σ eines Dauermagnetkreises nach dem «Symmetrischen Magnetsystem»:
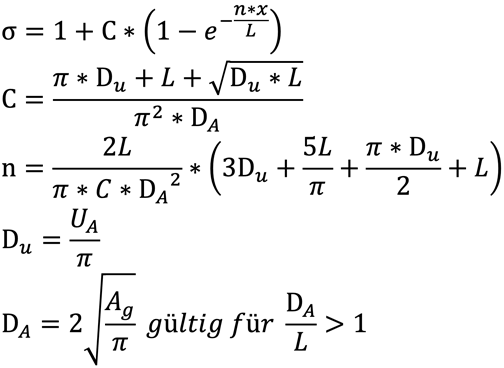
8. Transformationsformel von C. Schick
Zwischen dem totalen Streufaktor σ und dem praktischen Streufaktor σ_r besteht folgende Beziehung, gültig für den idealen Magnetkreis:
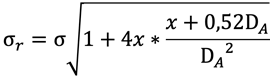
9. Formel der Kraft
Zwischen einem Magneten mit Querschnitt S und einem Polschuh aus Weicheisen, die sich berühren, hat man eine magnetische Induktion B, die als konstant angenommen werden kann. Die Kraft, mit der der Magnet den Polschuh anzieht, kann mithilfe folgender Formel berechnet werden:
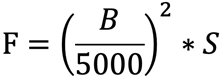
F = Kraft in kg
B = Induktion in Gauss
S = Fläche in cm2
(Wenn sich Magnet und Polschuh nicht berühren, ist es notwendig, zuerst die Streufaktoren zu berechnen, um einen genaueren Wert für die Induktion zu bekommen).
10. Kriterium von S. Evershed für statische Magnetsysteme
Um ein gegebenes Volumen an Magnetmaterial optimal auszunützen, muss der Arbeitspunkt Ha, Ba des Magnetsystems so gewählt werden, dass das Produkt Ha ∗ Ba das maximal mögliche Produkt ergibt.
11. Formel von E. A. Watson
Für Stahlmagnete gelten näherungsweise folgende Beziehungen:
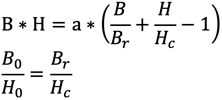
B0 und H0 entsprechen dem optimalen Arbeitspunkt und a ist eine Konstante.
12. Theorem von S. Earnshaw
Ein Permanentmagnet kann sich im Feld anderer Permanentmagnete nicht im stabilen Gleichgewicht befinden.
Magnete Einheiten
| Bezeichnung | Kurzzeichen | Einheit | Definition bzw. Äquivalenz |
| Länge | L | Meter (m) | Grundeinheit |
| Zeit | t | Sekunde (s) | Grundeinheit |
| Masse | m | Kilogramm (kg) | Grundeinheit |
| Kraft | F | Newton (N) | 1 N = 1 kg ∗ 1 m/s2 |
| F | Kilopond (kp) | 1 kp = 9,81 N | |
| Arbeit | E | Joule (J) | 1 J = 1 N ∗ 1 m |
| Leistung | P | Watt (W) | 1 W = 1 J/1 s |
| Strom | I | Ampere (A) | Grundeinheit |
| Spannung | U | Volt (V) | 1 V = 1 W/1 A |
| Magnetischer Fluss | Φ | Weber (Wb) | 1 Wb = 1 V ∗ 1 s |
| Φ | Maxwell (M) | 1 M = 10-8 Wb | |
| Magnetische Induktion | B | Tesla (T) | 1 T = 1 Wb/ m2 |
| B | Gauss (G) | 1 G = 10-4 T | |
| Magnetomotorische Kraft | MMF | Amperewindung (AW) | 1 AW = 1A ∗ 1 Wdg. |
| Θ | Gilbert (Gb) | 1 Gb = 0,796 AW | |
| Magnetische Feldstärke | H | Amperewindung/Meter (AW/m) | 1 AW/m = 1 AW/ 1 m |
| H | Oersted (Oe) | 1 Oe = 79,6 AW/m | |
| Reluktanz | R | Ampere/Weber (A/Wb) | 1 A ∗ Wb-1 = 1 mho/s |
| Elektrischer Widerstand | r | Ohm (n) | 1 Ω = 1 V/ 1 A |
| Elektrischer Leitwert | G | Siemens (S) | 1 S = 1 Ohm-1 = 1 mho |
Länge
Zeit
Masse
Kraft
Arbeit
Leistung
Strom
Spannung
Magnetischer Fluss
Magnetische Induktion
Magnetomotorische Kraft
Magnetische Feldstärke
Reluktanz
Elektrischer Widerstand
Elektrischer Leitwert
Die Magnetwerkstoffe und ihre Entstehung
AlNiCo
Die ersten Magnetwerkstoffe, die in der Industrie eingesetzt wurden, stammen aus den 1920er-Jahren. Bei dieser Magnetsorte handelt es sich um eine Stahlgusslegierung aus Aluminium, Nickel, Cobalt und Eisen und ist bekannt unter der Bezeichnung AlNiCo. Zum ersten Mal hergestellt wurde sie in England. Eines der wichtigen Markennamen war „Eclipse“.
Hartferrit
Während des 2. Weltkriegs durfte Deutschland keine Legierungsmaterialien für Stahl importieren. Deshalb erfand man im Deutschen Reich eine neue Magnetmaterialkategorie, den Ferrit. Man stellte den neuen Werkstoff her, indem man Eisenoxid – ein Abfallprodukt aus der Eisenverhüttung¬ – mit den frei verfügbaren Schwermetallen Barium oder Strontium sinterte. Die etablierten Magnethersteller in England bezeichneten den Werkstoff als „dirty magnets“, da dieser in ihren Augen schmutzig in der Verarbeitung war. Das neue Material stellte aus magnettechnischer Sicht keine Revolution dar und war von eher minderwertiger Qualität. Dennoch brach in den 1950ern ein Siegeszug los, da es zu einem deutlich günstigeren Preis als andere Magnetwerkstoffe hergestellt werden konnte.
Plastoferrit und kunststoffgebundene Ferrite
Kurz nach der Erfindung von Hartferrit wurde ein neuer Werkstoff geschaffen, der flexible Magnet.
Man bekommt ihn, indem man Ferritmagnetpulver mit hohem Füllgrad in eine Kunststoffmatrix einbettet. Die Leistungsfähigkeit der magnetischen Eigenschaften verringert sich dadurch um ca. 30 %, das Material wurde aber genau deswegen gerne und viel in der Werbung und für Lagerbeschriftungen verwendet.
Als Spritzformen oder Pressling hat das Material auch den Weg in den Elektromotorenbau gefunden. Das Material ist als Duroplast konzipiert und entsprechend hart und formstabil. Im Speziellen konnten damit Zahnräder urgeformt oder Achsen eingespritzt werden.
Samarium-Cobalt
Dieses Material wurde Ende der 1960er-Jahre in der Schweiz erfunden. Mit Samarium-Cobalt schaffte man einen grossen materialtechnischen Sprung, denn dieser Magnetwerkstoff erzielte eine um ein Mehrfaches grössere magnetische Leistung als Hartferrit und AlNiCo. Während der ersten zehn Jahre wurde der Werkstoff nur in Spezialapplikationen verwendet. Noch heute ist dieser Werkstoff dank seiner speziellen Eigenschaften im Temperaturverhalten, in der magnetischen Stabilität und der Oxidationsbeständigkeit ein wichtiges Material in der Industrie.
Neodym (Supermagnete)
Neodym ist der heute unangefochtene Spitzenreiter unter den Magnetwerkstoffen. Auch hier fand der Siegeszug über das hervorragende Preis-Leistungs-Verhältnis statt. Der Werkstoff hat jedoch ein paar Nachteile: Da das Halbelement Bor eingebaut ist, ist die Legierung instabil und es bedarf einiger kniffliger Methoden, um die Materialien anwendungsstabil herstellen zu können. Wäre die Leistung gegenüber allen anderen Magnetmaterialien nicht derart besser und der Preis nicht so tief, würde niemand eine solch instabile Legierung einsetzen.
Der Pferdefuss an diesem Magnetmaterial ist jedoch die Rohstoffquelle und dessen Raffinierung. 97 % der weltweiten Rohmaterialschürfung findet in China statt sowie über 60 % der Raffinierung. Dies führt zu einer ausserordentlichen Abhängigkeit von chinesischen Lieferanten. Auch muss man die Kontaminierung durch radioaktive Nebenprodukte berücksichtigen, die bei der Gewinnung dieser Seltenen Erde entstehen. Der Umweltschaden könnte immens werden, wie bereits in Malaysia vor ein paar Jahren geschehen. Problematisch ist auch, dass das Magnetmaterial hauptsächlich für Spiel und Spass eingesetzt wird – lohnt es sich wirklich, dass China dafür seine Ressourcen ausbeutet und billigst auf den Markt wirft?
Die Abhängigkeit der westlichen Welt ist derart gross, dass bereits nach Alternativen geforscht wird, die es erlauben, ohne diesen Magnetwerkstoff auszukommen. Das betrifft vor allem die Automobilindustrie mit den Elektromotoren. Der Automobilhersteller Tesla aus den USA hat direkt auf dauermagnetfreie Asynchronmotoren gesetzt. Die europäischen Hersteller hingegen setzen auf die permanentmagnetbestückten Synchronmotoren.
Plasto-Neodym
Wie das Plastoferrit ist auch dieses Materialsubstitut als flexibles Magnetmaterial in den 90ern entstanden. Plasto-Neodym erreicht gegenüber dem Plastoferrit eine zehnmal grössere Haftkraft.
Zukunft der Magnetwerkstoffe
Es ist in absehbarer Zeit keine neue Magnetmaterialgeneration in Sicht. Es wird hauptsächlich geforscht, um schwer erhältliche Rohstoffe zu ersetzen und Magnetmaterial optimal zu recyceln. Die stark oxidierenden Seltenen Erden kann man aber für das Recycling nicht ohne Weiteres extrahieren. Der Fokus muss deshalb auf die Wiederverwendbarkeit der Magnete gesetzt werden. Bisher ist dieser Ansatz nur in den grossen Generatoren der Windturbinen geglückt. Hier werden grosse Magnetsegmente mittels mechanischer Verschraubung so eingebaut, dass der Magnet unbeschädigt wieder ausgebaut und neu verwendet werden kann.
In der additiven Herstellung ist gerade ein Kaltspritzverfahren in Entwicklung. Das NRC–Forschungszentrum in Kanada erwartet, dass sie damit gegenüber gesinterten Seltenen Erden eine höhere Festigkeit und komplexere Aufbaumöglichkeiten erreichen sowie gute magnetische Werte und eine höhere Korrosionsbeständigkeit. Ausserdem müssen Systemaufbauten in Kombination mit Polrückschlüssen aus Eisen nicht mehr zusammengesetzt bzw. verklebt werden.
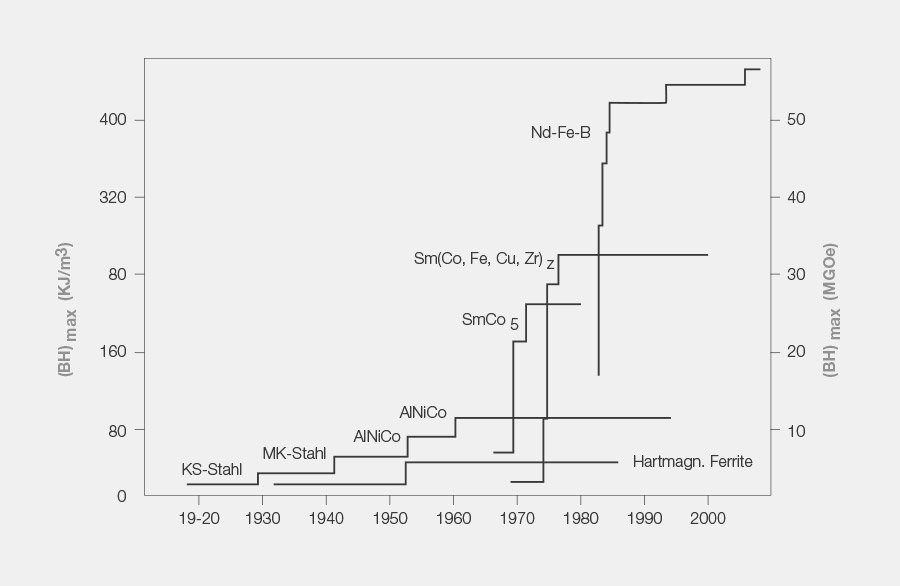
Verfügbarkeit und Entwicklung der Magnetwerkstoffe
Die Hauptgruppen der Magnetwerkstoffe sind in einer Reihe von Untersorten segmentiert.
In diesen Segmenten spiegeln sich hauptsächlich die Entwicklungsstufen der jeweiligen Herstellungsmöglichkeiten wider. Die Eigenschaften zielen vornehmlich auf das Herbeiführen höherer Energieprodukte (BHmax) ab sowie auf das Erhöhen der Remanenz (Br) und der Koerzitivkraft (Hcj). Der Energieinhalt und die Remanenzerhöhung sind auf die Steigerung der Leistungsfähigkeit ausgerichtet. Bei der Koerzitivkraft (Widerstandskraft) wird auf die Verbesserung bzw. Erhöhung der Einsatztemperatur und der sektoriellen Entmagnetisierung der Magnete in Elektromotoren abgezielt, was auch als Footprint bezeichnet wird.
Magneteigenschaften
AlNiCo
Die AlNiCo-Magnete zeichnen sich besonders durch folgende Eigenschaften aus:
- Temperaturstabilität 0,02 % pro °C
AlNiCo-Magnete sind deshalb bestens geeignet, in Wägesystemen und Sensoranwendungen eine Temperaturstabilisierung herbeizuführen. - Hohe Einsatztemperatur bis 500 °C
In vereinzelten Anwendungen werden Temperaturen erreicht, welche die Schwelle der nächstliegenden Materialklasse (SmCo mit 350 °C) überschreiten. AlNiCo ist der einzige Werkstoff, den man in diesen Fällen einsetzen kann, z. B. für Halterungen bei PVD-Beschichtungsprozessen. - Magnetische Stabilität
Die Magnetisierung verhält sich sehr stabil, die Voraussetzung ist jedoch eine Stabilisierungsentmagnetisierung. Gegenüber Fremdfeldern ist der Werkstoff sehr empfindlich, hier bedarf es grosser Aufmerksamkeit.
Hartferrit
Ferrite haben folgende Eigenschaften:
- höchster Temperaturgang aller Werkstoffe bei 0,2 % pro °C
- geringe Einsatztemperatur, Bandbreite von -20 °C bis 220 °C
- geringes Energieprodukt, schwache Leistung
- hohes Gewicht im Verhältnis zur Leistung
- oxidationsbeständig
- elektrisch isolierend, 105 Ohm/m
- leicht magnetisierbar, 1 Tesla Magnetisierfeldstärke
- günstiger Preis
Samarium-Cobalt
Das ist der Problemlöser unter den Werkstoffen – er bietet sich an für heikle Anwendungen aller Art und vereint so ziemlich alle positiven Eigenschaften aus allen Werkstoffklassen. Aber Achtung: Es gibt zwei Hauptklassen, den Sm1Co5 und der Sm2Co17. Der 2:17 besitzt eine höhere Remanenz und ist günstiger im Preis. Im Gegensatz zum 1:5 benötigt er aber eine sehr hohe Magnetisierfeldstärke – über 5 Tesla gegenüber 2,5 Tesla beim 1:5er. Im flüssigen Stickstoff oxidiert der 2:17er.
Folgende Eigenschaften besitzt der Samarium-Cobalt-Magnet:
- hohe Temperaturbeständigkeit, von -273,15°C (absoluter Nullpunkt) bis 350 °C
- kleiner Temperaturgang, 0,035 % pro °C
- beste magnetische Stabilität
- oxidationsresistent
- enge Toleranzen in den Abmessungen möglich
- Sprödheit des Materials
- hohe Magnetisierungsfeldstärken bis 5,5 Tesla (2:17)
Neodym-Eisen-Bor
Der meistverwendete Werkstoff, bei dem das Preis-Leistungs-Verhältnis unübertroffen ist. Es gibt viele Unterkategorien und da die Herstellung dieser Magnete fast ausschliesslich in China stattfindet, hat sich die Bezeichnung der Materialien aus dieser Region eingebürgert. Die Leistungsklassen werden in den alten CGS-Einheiten angegeben – MGOe (Mega-Gauss-Oersted) –, womit das maximale Energieprodukt bezeichnet wird. Ausserdem ist die Angabe der Koerzitivkraft empirisch gewachsen und mit der Entwicklung des Materials wurde das Temperaturverhalten laufend erhöht.
Folgende Eigenschaften besitzt der Neodym-Magnet:
- gute Temperaturbeständigkeit, von -196 °C (flüssiger Stickstoff) bis 240 °C
- mittlerer Temperaturgang, 0,1 – 0,12 % pro °C
- gute magnetische Stabilität
- sehr oxidationsanfällig
- nachteilige Beschichtung erforderlich
- nur angemessene Toleranzen in den Abmessungen wegen der Beschichtung
- Magnetisierungsfeldstärken ab 1,5 Tesla (Spezialmaterial), typisch 2,5 Tesla
Für die bildliche Ausdrucksweise der Chinesen werden quantitative Begriffe verwendet.
Die Bezeichnungen setzen sich zusammen aus drei Komponenten:
Der Anfangsbuchstabe steht für das Material, d. h. N für Neodym.
Diverse Händler verwenden eigene Bezeichnungen, die auf den Markt einschränkend wirken sollen, wie z. B. BMN, GSN, REFeB, VACODYM usw. Grundsätzlich handelt es sich aber um dieselben Werkstoffe.
Die Zahl steht für das Energieprodukt, z. B. 35 für BHmax. in MGOe.
Der Buchstabe steht für die Koerzitivkraft bzw. Temperatur: H für 120 °C.
Tabellarische Ausführung mit frei zusammengestellten Beispielen:
| Energieinhalt | Temperatur | Einsatztemperatur | Ausdrucksweise Temperatur |
|---|---|---|---|
| 35 | 80 °C | Standard | |
| 38 | M | 95 °C | Medium |
| 40 | H | 110 °C | High |
| 42 | SH | 150 °C | Super-High |
| 38 | UH | 180 °C | Ultra-High |
| 35 | EH | 200 °C | Extremely-High |
Die weitere Fortsetzung folgt dem Alphabet:
30 AH 220 °C
25 BH 240°C
Zu beachten sind die Oxidationseigenschaften. Hier gibt es grosse Unterschiede, selbst wenn in letzter Zeit auch hier starke Fortschritte gemacht und die problematischsten Legierungen eliminiert wurden. Um das Oxidationsverhalten zu beziffern, wird der sogenannte HAST-Test (Highly Accelerated Test) verwendet. Das ist nichts anderes als ein Dampfkochtopf, in welchen das unbeschichtete Magnetmaterial eingebracht wird. Dieses wird über eine bestimmte Zeit einem atmosphärischen Dampfdruck von ca. 2,6 bar ausgesetzt. Der Oxidationsanteil, der dadurch entsteht, wird abgetragen und das Gewicht gemessen.
Der Test war ursprünglich als eine verschärfte und beschleunigte Feuchteprüfung gedacht. Diese erlaubt es, den schädlichen Einfluss von feuchter Wärme auf die zu prüfenden Probanden (meistens elektrotechnische, nicht hermetisch verschlossene Bauteile) innerhalb kürzester Zeit zu beurteilen.
Oxidation nach «HAST»

«Highly Accelerated Stress Test» 130 °C / 95 % Feuchte und 2,6 bar Druck
Herkömmliches Neodym-Magnetmaterial „Standard“ weist die folgenden Abtragungswerte auf: 10 mg/cm2 in 6 Tagen und 100 mg / cm2 in 10 Tagen.
Die Maurer Magnetic AG liefert standardmässig eine Qualität von 2 mg/cm2 in 7 Tagen.
Die besten Eigenschaften liegen zurzeit bei 2 mg/cm2 in 20 Tagen. Dies entspricht der L-Serie für „low weight loss“ und der L-T-Serie für „low weight loss“ und „low temperature coefficient“. Diese Serien sind ab ca. 300 kg Losgrösse erhältlich.

Generell werden Neodym-Magnete galvanisch oder organisch beschichtet. Die verschiedenen Beschichtungen sind auf verschiedene Bedürfnisse ausgerichtet. Meistens werden Nickelbeschichtungen angeboten. Die Verbreitung dieser Beschichtung ist darauf zurückzuführen, dass ein Magnet schön aussehen soll. „shiny magnet“ nennen das die Hersteller in China – in den Anfängen war eine glänzende Beschichtung gleichbedeutend mit guter Qualität. Die Beschichtung mit Nickel bietet einen guten Schutz, ist jedoch für Verklebungen nicht sonderlich geeignet. Besser ist eine zusätzliche Zinnschicht oder eine Beschichtung mit Epoxy. Beschichtungen aus Zink sind ebenfalls zu empfehlen und haben sich bereits als Standard etabliert.
Maurer Magnetic nutzt verschiedene Beschichtungen, um die im Standardprogramm angebotenen Neodym-Magnete zu differenzieren. Dimensionen gleicher Grösse sind in den Materialien N35 / N48 / und N45SH ab Lager lieferbar. Der N35 ist mit Zink, N48 mit Nickel und N45SH zusätzlich zu Nickel mit Zinn beschichtet.
Der grösste Anteil der Lieferungen an die Industrie ist jedoch kundenspezifisch – Material, Form, Beschichtung, Magnetisierung, Verpackung usw. bestimmt der Kunde.