Pour beaucoup, les aimants permanents ne manquent pas de mystère.
«À quoi servent les aimants permanents ?», entend-on souvent. Peu de gens le savent, mais les aimants permanents sont déjà devenus indispensables dans la technologie moderne et font déjà partie de notre quotidien. Ils figurent dans les écouteurs ou haut-parleurs, les smartphones, les entraînements électriques des automobiles électriques, les vélos électriques, les trottinettes électriques, les fauteuils roulants électriques, les éoliennes qui produisent de l’électricité, pour ne citer que quelques exemples d’application. Dans le domaine de la technologie, les aimants permanents sont utilisés pour les appareils servant aux mesures électriques et mécaniques, comme les transducteurs acoustiques, les transducteurs électromécaniques ou encore les éléments de machine, où l’on exploite leur force magnétique.
Les aimants permanents sont également devenus incontournables dans les domaines de la médecine, de la biologie et de la physique nucléaire. De par leur vaste diffusion et leur prix très raisonnable, les aimants en néodyme en particulier, également appelés super aimants, sont désormais très présents dans les domaines des jeux et des divertissements.
Malgré cette polyvalence, relativement peu de techniciens possèdent des connaissances théoriques approfondies et maîtrisent l’utilisation des aimants permanents. Cette situation est sans doute due au fait que, malheureusement, seules quelques universités et écoles supérieures enseignent les propriétés des aimants permanents.
Terminologie de base en matière de magnétisme
1. Flux magnétique
Pour mieux comprendre ce qu’est le champ magnétique autour d’un aimant permanent magnétisé, il est possible de se le représenter comme un espace rempli de lignes de force magnétique. Les lignes de force sortent au niveau du pôle nord de l’aimant et forment un grand arc dans l’espace qui se poursuit jusqu’au pôle sud. Chaque ligne de force constitue ainsi son propre circuit.
Le flux magnétique est constitué par l’ensemble des lignes de force.
Le symbole du flux magnétique est Φ (Phi) et représente le nombre total de lignes de force d’un aimant.
L’unité du flux magnétique est la suivante:
1 Maxwell = 1 ligne de force
Φ = B ∗ Fm
Flux magnétique total = Flux magnétique total = Rémanence en Gauss * Surface (section) de l’aimant en cm2
2. Rémanence
Plus l’effet magnétique d’un champ magnétique est fort à un endroit donné, plus vous devez vous imaginer, à cet emplacement, un tracé dense des lignes de force.
La rémanence ou l’induction correspond à la densité des lignes de force.
Le symbole de la rémanence est B et représente le nombre de lignes de force passant verticalement à travers une zone de 1 cm2.
L’unité de la rémanence ou de l’induction est la suivante:
1 Gauss = 1 ligne de force par cm2 = 10-8 volts/seconde par cm2
Rémanence = (Flux magnétique total en Maxwell)÷(Surface en cm2 à travers laquelle le flux magnétique s’échappe)
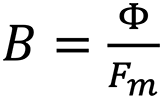
3. Force coercitive
On peut se représenter la force coercitive comme la résistance à la démagnétisation par un champ magnétique externe. Il s’agit de la durabilité des aimants permanents par rapport à une force démagnétisante.
Le symbole de la force coercitive est le signe Hc et représente la taille d’un champ externe opposé à un aimant permanent, capable de supprimer totalement la rémanence de l’aimant permanent.
L’unité de la force coercitive est la suivante:
1 Oersted ≅ 0,8 AW/cm (ampères-tours par cm)
4. Force magnétomotrice
Après magnétisation, une tension magnétique est présente à l’intérieur de chaque aimant permanent, qui peut être considérée comme étant à l’origine du champ magnétique généré dans l’espace entourant l’aimant.
La force magnétomotrice (MMF) correspond à la tension magnétique totale ou à la force d’entraînement magnétique totale d’un aimant permanent, qui a pour effet de remplir l’espace autour de l’aimant de lignes de force.
Le symbole de la force magnétomotrice est Θ (Thêta) et représente la tension magnétique totale disponible.
L’unité de la force magnétomotrice est la suivante:
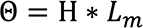
1 Gilbert = 1 Oersted × cm ≅ 0,8 ampères-tours
Force magnétomotrice = Intensité du champ coercitif * longueur de l’aimant en cm
5. Intensité du champ coercitif
Plus les lignes de force d’un champ magnétique sont éloignées dans l’espace, plus on peut s’imaginer un champ magnétique intense.
L’intensité du champ coercitif désigne la tension magnétique par unité de longueur d’un champ magnétique.
Le symbole de la force coercitive est H et représente la tension magnétique ou la force magnétomotrice contenue dans 1 cm de longueur d’un aimant permanent.
L’unité de l’intensité du champ coercitif est la suivante:
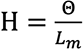
1 Oersted ~ 0,8 AW/cm (ampères-tours par cm)
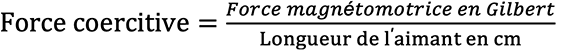
Le rapport avec la taille habituelle de l’ampère-tour dans la théorie de l’électricité est le suivant:
La tension magnétique d’une bobine parcourue par un courant électrique correspond à la tension magnétique d’un aimant permanent. La tension magnétique d’une bobine ou de sa force magnétomotrice est calculée sur la base de la formule I * n / L = At/cm, où I correspond au courant circulant en ampères, n au nombre de tours du fil et L à la longueur de la bobine en cm, dont résulte le produit ampères-tours/cm.
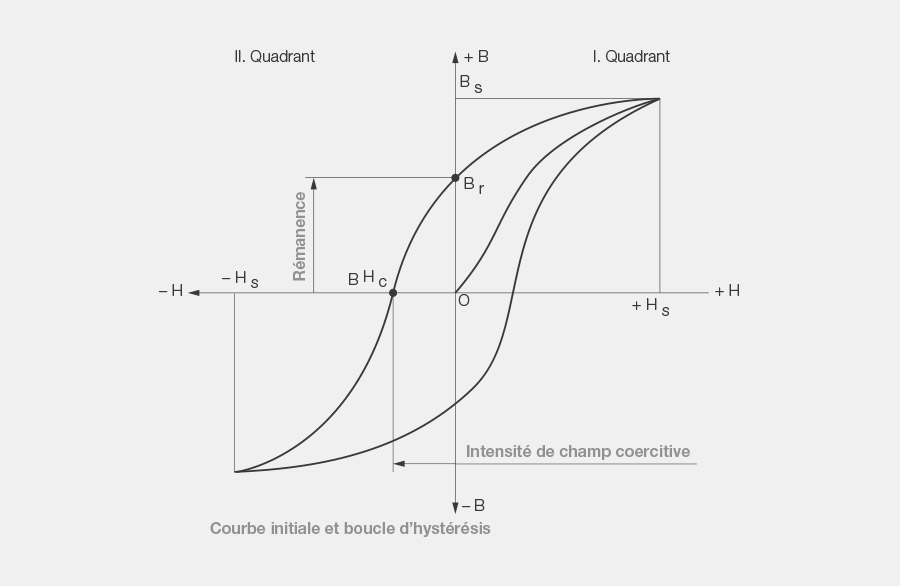
6. Boucle d’hystérésis
La boucle d’hystérésis correspond à la représentation graphique du comportement d’un matériau dans un champ magnétique externe. À ces fins, la rémanence B est saisie en ordonnée et l’intensité du champ coercitif H, en abscisse dans un système de coordonnées rectangulaires. À présent, le matériau servant de base à la détermination de la boucle d’hystérésis est exposé à un champ magnétique croissant. Par réaction, la rémanence augmente dans l’échantillon. Si cette augmentation est saisie dans le premier quadrant du système de coordonnées, on obtient ce que l’on appelle la courbe initiale qui, avec + HS (intensité du champ de saturation), atteint une valeur de saturation standard pour chaque matériau ferromagnétique. Cette saturation porte également le nom d’induction maximale.
Si l’intensité du champ magnétique externe diminue à présent, la rémanence dans les matériaux à magnétisme permanent ne baisse pas sur la courbe initiale. Les valeurs d’induction sont plus élevées et il reste une valeur finie Br lorsque le champ magnétique externe (H = 0) est complètement coupé. Il s’agit de l’induction rémanente ou du magnétisme résiduel au point de rémanence.
Si la polarité du champ externe est à présent inversée, entraînant une augmentation du champ, la rémanence B continue de diminuer jusqu’à disparaître complètement dans ce que l’on appelle le point coercitif BHc (B = 0).
Les matériaux modernes du groupe des terres rares assurent un ancrage plus profond des dipôles magnétiques et leur polarité n’est inversée qu’en présence d’un champ magnétique externe plusieurs fois supérieur. Cette valeur est déterminante pour la ténacité de remagnétisation des matériaux magnétiques dans des champs opposés puissants et pour la résistance thermique, par exemple, dans les moteurs électriques. La valeur est utilisée pour calculer les circuits magnétiques.
Le champ magnétique se renforçant encore, B circule à présent avec le signe inversé sur une branche négative jusqu’à un point de saturation opposé au premier. Si l’opération est à présent répétée avec un nouveau changement de polarité, B retourne jusqu’au premier point de saturation en suivant une trajectoire symétrique par rapport à la première courbe. La boucle ainsi fermée est appelée boucle d’hystérésis. La surface qu’elle englobe représente l’énergie convertie en chaleur lors de la remagnétisation.
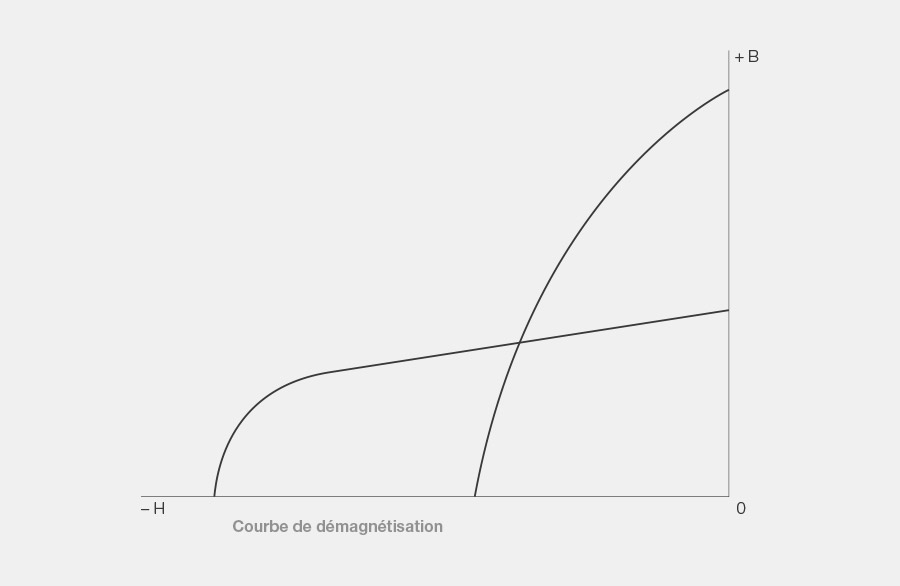
7. Courbe de démagnétisation
Essentielle pour les aimants permanents, cette caractéristique est une section de la boucle d’hystérésis. Elle illustre l’évolution de B dans le deuxième quadrant en présence d’une intensité de champ croissante opposée à la magnétisation. Il s’agit d’un critère extrêmement important pour la qualité d’un matériau magnétique et pour le calcul des aimants permanents.
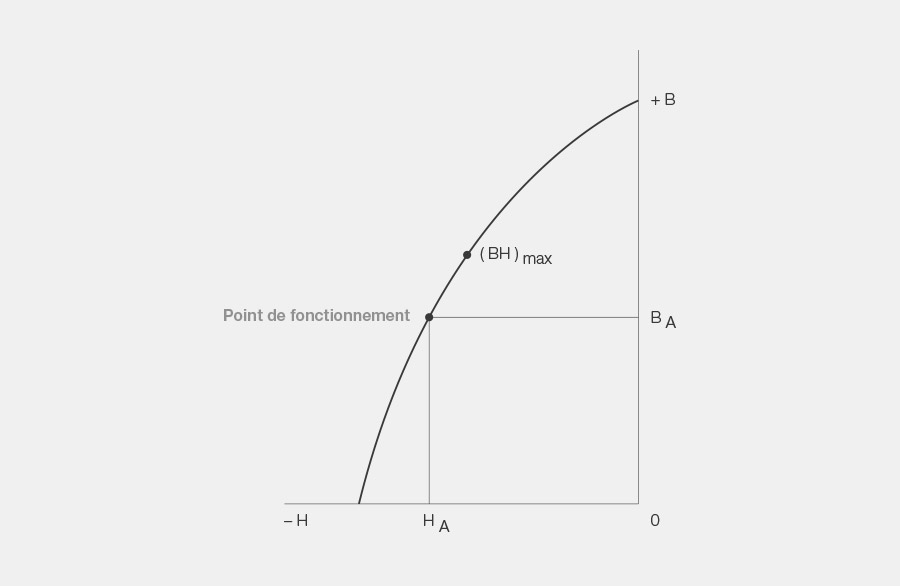
8. Point de fonctionnement
Le mécanisme de réglage automatique du point de fonctionnement d’un aimant est relativement compliqué. Dans la pratique, l’explication qualitative suivante suffit:
Après coupure du champ magnétique externe généré par le courant, le point de fonctionnement d’un aimant qui a été magnétisé dans une culasse ou une bobine de solénoïde se situe au point de rémanence Br. Sous l’effet de l’ouverture de la culasse ou après l’impulsion de magnétisation, un entrefer est généré dans le circuit magnétique, complètement fermé jusqu’à présent. Des pôles magnétiques se forment au niveau des surfaces de l’entrefer. Ces pôles « magnétisent » l’entrefer. Autrement dit, ils émettent un flux magnétique et génèrent un champ magnétique dans l’entrefer. Parallèlement, l’aimant se démagnétise autant que nécessaire pour générer le champ magnétique en fonction de la longueur de l’aimant à air.
La force magnétomotrice requise pour créer le champ est générée par l’énergie mécanique nécessaire à l’ouverture du circuit magnétique ou au retrait de l’aimant de la culasse. Cette force magnétomotrice conduit l’aimant à se démagnétiser étant donné qu’elle est dirigée dans le sens opposé à la magnétisation. Par conséquent, la rémanence B se déplace depuis le point d’induction Br sur la courbe de démagnétisation dans la direction H jusqu’à un nouveau point BA, le point de fonctionnement, dont la position dépend de l’ouverture du circuit magnétique et de l’intensité de la force coercitive du matériau magnétique. Sa position dépend de la longueur d’aimant sélectionnée en fonction de la force coercitive.
Le point de fonctionnement d’un aimant sur la courbe de démagnétisation indique son état magnétique actuel. Le point de fonctionnement BA et le point de fonctionnement coercitif HA sont associés au point de fonctionnement.
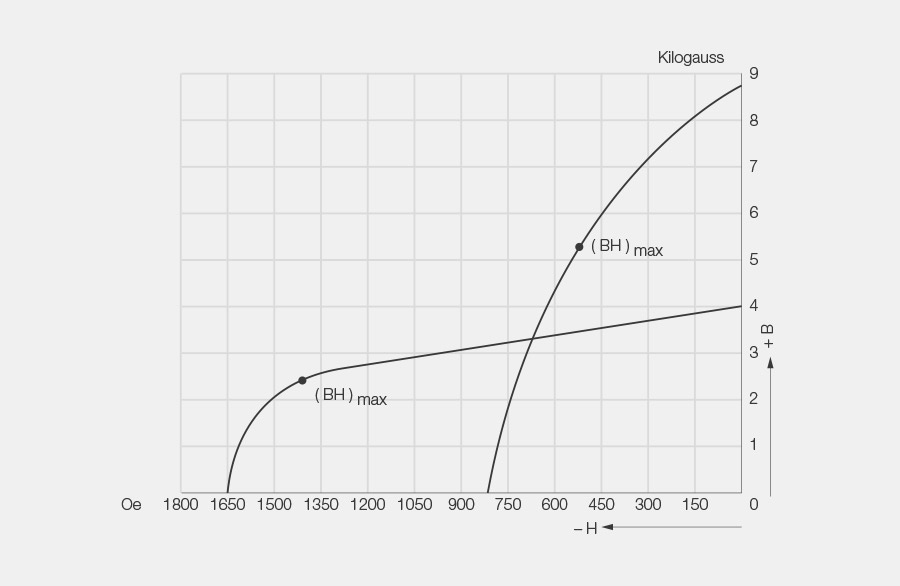
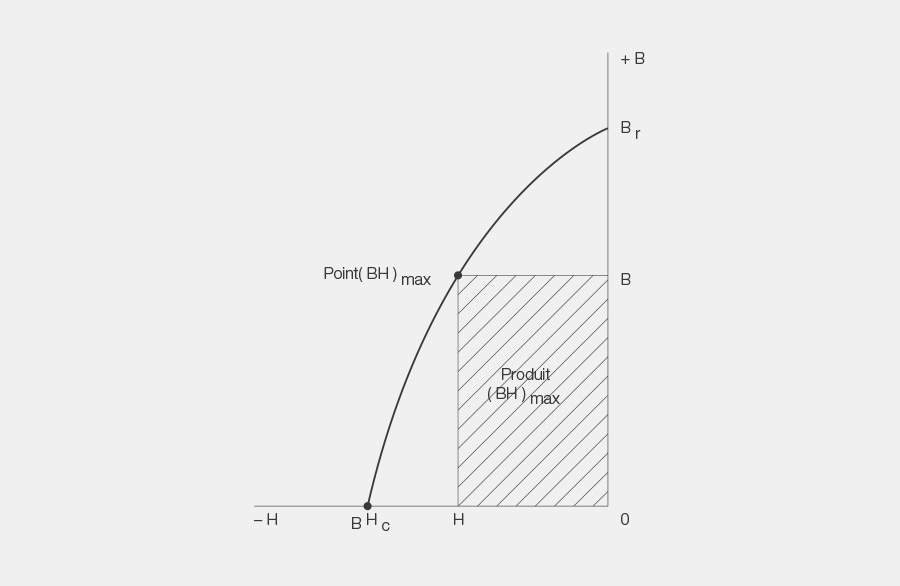
9. Point (BH)max
Sur la courbe de démagnétisation, le point (BH)max là où les valeurs associées de la rémanence et de la force coercitive, multipliées entre elles, donnent le plus grand produit
10. Produit énergétique
Ce produit est calculé à partir des valeurs associées de la rémanence et de la force coercitive, qui peuvent être lues sur la courbe de démagnétisation. Il indique l’énergie rémanente d’un matériau magnétique.
Pour utiliser correctement un matériau magnétique, il est conseillé de concevoir le circuit magnétique de manière à ce que l’aimant fonctionne au point (BH)max car il génère un maximum d’énergie dans l’entrefer pour un volume donné de matériau magnétique.
Le produit (BH)max indique la plus capacité de travail maximale d’un matériau magnétique par rapport à l’unité de volume.
Le symbole du produit énergétique est (BH)max et correspond au produit maximal (BA * HA) d’un matériau magnétique.
11. Flux de fuite
La plupart des aimants permanents ne fonctionnent cependant pas au même point de fonctionnement sur toute leur longueur. L’intégralité du flux magnétique ne traverse l’aimant que dans la zone neutre (à mi-chemin entre les deux pôles). L’ensemble de ce flux magnétique se compose du flux utile dans un entrefer et du flux de fuite inévitable. Si l’on veut qu’un aimant fonctionne au même point de fonctionnement sur toute sa longueur, il doit être plus épais vers le centre afin de contrer le flux de fuite. Il s’agit là de l’une des raisons pour lesquelles les branches sont coniques sur de nombreux aimants en fer à cheval.
Dans la pratique, en revanche, on suppose que les aimants fonctionnent au même point de fonctionnement sur toute leur longueur, autrement dit, qu’ils assurent le même flux magnétique partout. La plupart du temps, ce postulat est assez précis, mais justifie cependant que la perte de fuite soit prise en compte dans tous les calculs, conceptions et mesures.
12. Réluctance
La réluctance est la résistance magnétique d’un circuit magnétique. Elle résulte de toutes les résistances partielles magnétiques des différentes pièces qui constituent le circuit magnétique. La valeur de réluctance est utilisée pour déterminer le flux magnétique nécessaire dans une partie donnée d’un circuit magnétique, par exemple, dans un entrefer. Le symbole de la réluctance est R.
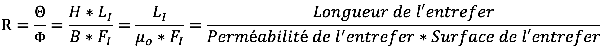
13. Calcul des aimants permanents
Lors du calcul des aimants permanents, il est préférable de partir de la réluctance spécifique ou de sa taille réciproque, à savoir la perméance spécifique. Lors du calcul de la réluctance ou de la perméance spécifique, le plus difficile consiste à calculer les pertes de fuite et de potentiel. Certes, il existe des formules de calcul de ces pertes pour les circuits magnétiques les plus courants, mais soit ces formules sont beaucoup trop compliquées, soit les calculs sont réalisés avec des formules simplifiées et ne permettent d’obtenir que des valeurs approximatives. Par conséquent, il est peine perdue de tenter de calculer un circuit magnétique avec une précision à 5 décimales si seuls des facteurs approximatifs de perte de fuite et de potentiel sont disponibles. Même si le calcul de ces facteurs est supposé être correct, il est essentiel de vérifier les calculs par des mesures sur un modèle.
En général, on peut dire que le facteur de perte de fuite ρ1 (rho1) est, la plupart du temps, compris entre 2 et 10. La section donnée de l’entrefer utile doit être multipliée par cette valeur afin de compenser pour les pertes de fuite inévitables de chaque circuit magnétique. Le facteur de perte de potentiel ρ2 (rho2) est beaucoup plus faible et se situe généralement entre 1,1 et 1,5. Ce facteur doit être multiplié par la longueur de l’entrefer utile donné afin de compenser les pertes de force magnétomotrice (MMK) qui se produisent en raison du pliage des lignes de force et des pertes qui surviennent aux jointures du circuit magnétique.
Dans la littérature moderne, le facteur de perte de fuite est désigné en tant que σ (sigma) et le facteur de perte de potentiel, en tant que τ (tau).
Il ne faut pas confondre σr et σ. Le facteur de fuite pratique est σr = Φi ÷ Φen. Le facteur de fuite total est σ = Φi ÷ Φe . À ces fins, Φen correspond au flux net dans l’entrefer, Φi, au flux dans les aimants et Φe, au flux total qui traverse l’entrefer.
Comme il est si difficile de déterminer les facteurs de perte précis, les circuits magnétiques permanents ne doivent pas être construits sur la seule base de valeurs calculées. Les valeurs empiriques et résultats des mesures sur les modèles expérimentaux doivent également être pris en compte. En raison de ces difficultés, la construction de cercles magnétiques permanents n’est pas une simple opération mathématique, mais véritablement un art qui, en tant que tel, requiert talent et expérience.
Les programmes de calcul informatisés modernes sont en mesure de calculer les systèmes à aimants permanents de manière très fiable dans leur structure. Cette tâche est déjà plus ardue avec les systèmes construits avec des aimants multipolaires ou regroupant plusieurs aimants multipolaires.
Les programmes de calcul ne peuvent pas encore proposer la structure de base et la construction d’un système magnétique. Il reste encore à construire le système magnétique destiné à un usage ou à des propriétés spécifiques.
Pourquoi tant d’alliages magnétiques?
Les nombreuses nuances des matériaux magnétiques isotropes, anisotropes et à cristaux orientés n’auraient bien évidemment pas été fabriquées sans raison. Un aimant peut, par exemple, présenter uniquement un volume minimal absolu, ou doit conduire le flux magnétique à travers un grand entrefer, ou doit résister à des températures élevées, ou doit être très peu coûteux, ou doit pouvoir être magnétisé de manière multipolaire sur la circonférence ou doit encore résister à des champs de démagnétisation. Toutes ces exigences ne peuvent être satisfaites que par un matériau magnétique adapté à l’utilisation prévue.
Formules magnétiques
1. Loi de BIOT-SAVART
Un conducteur traversé par un courant génère un champ magnétique en tout point P en dehors du trajet du courant. Pour un conducteur s’étendant sur une longueur infinie, la formule intégrale est la suivante:
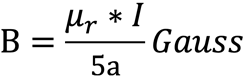
I = courant en ampères, a = distance entre le point P et le conducteur en cm, μr = perméabilité relative
2. Loi de LAPLACE
Un conducteur traversé par un courant de longueur L dans le champ d’autres conducteurs traversés par un courant ou aimants permanents subit une force F. La formule est la suivante:
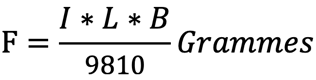
I = courant en ampères, L en cm, B = induction en Gauss
Valable pour B perpendiculaire à L, où F est à son tour perpendiculaire à L et B. La règle de la main gauche s’applique : B en direction de l’index, la direction du courant correspond au majeur, la force, au pouce.
3. Lois de KIRCHHOFF
En chaque point d’un circuit magnétique, la somme des flux entrants ∑Φe est égale à la somme des flux sortants ∑Φa
Dans un système magnétique fermé en soi, la somme des tensions partielles magnétiques (Tension partielle=Φ * R,autrement dit, flux * réluctance) est égale à la somme des forces magnétomotrices actives dans le système.
Ces lois sont parfois appelées lois de Houston pour les cercles magnétiques.
4. Formule de la réluctance
Une structure prismatique de longueur L et de section S présente une résistance magnétique ou une réluctance R.
La formule suivante s’applique:

5. Formule de R. K. Tenzer
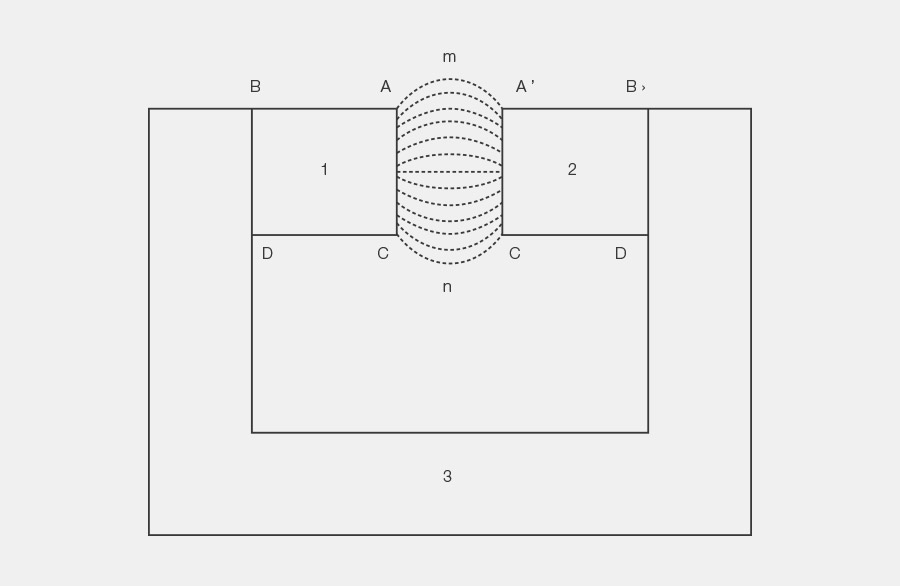
Le facteur de fuite pratique d’un circuit magnétique permanent selon l’image « système magnétique symétrique » est obtenu approximativement par la formule suivante:
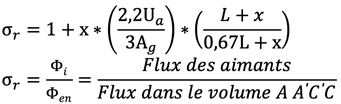
6. Équation différentielle de C. Schick
Pour le facteur de fuite total d’un circuit magnétique permanent idéal selon l’image « système magnétique symétrique », l’équation différentielle suivante s’applique:
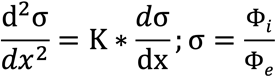
x=Longueur de l’entrefer, K=Constante
Φe= Flux dans le volume A m A’C’ n C
Φi=Flux dans les aimants
7. Formules de C. Schick
Les relations suivantes s’appliquent pour le facteur de fuite total σ d’un circuit magnétique permanent selon l’image «système magnétique symétrique»:
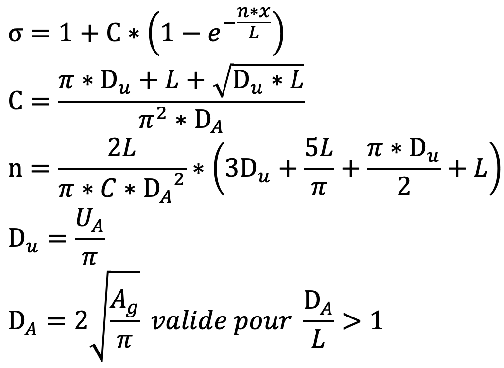
8. Formule de transformation de C. Schick
La relation suivante existe entre le facteur de fuite total σ et le facteur de fuite pratique σr. Elle est valable pour le circuit magnétique idéal:
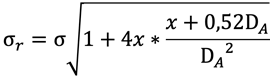
9. Formule de la force
Entre un aimant de section S et une pièce polaire en fer doux qui se touchent, on obtient une induction magnétique B que l’on peut supposer constante. La force avec laquelle l’aimant attire la pièce polaire peut être calculée au moyen de la formule suivante:
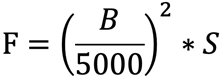
F = force en kg
B = induction en Gauss
S = surface en cm2
(Si l’aimant et la pièce polaire ne se touchent pas, il est nécessaire de commencer par calculer les facteurs de fuite afin d’obtenir une valeur plus précise pour l’induction).
10. Critère de S. Evershed pour les systèmes magnétiques statiques
Pour exploiter au mieux un volume donné de matériau magnétique, le point de fonctionnement Ha, Ba du système magnétique doit être sélectionné de sorte que le produit Ha * Ba donne le produit maximal possible.
11. Formule de E. A. Watson
Les relations suivantes s’appliquent approximativement aux aimants en acier:
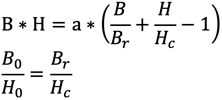
B0 et H0 correspondent au point de fonctionnement optimal et a est une constante.
12. Théorème de S. Earnshaw
Un aimant permanent ne peut pas se trouver en équilibre stable dans le champ d’autres aimants permanents.
Unités magnétiques
| Désignation | Abréviation | Unité | Définition ou équivalence |
| Longueur | L | Mètre (m) | Unité de base |
| Heure | t | Seconde (s) | Unité de base |
| Masse | m | Kilogramme (kg) | Unité de base |
| Force | F | Newton (N) | 1 N = 1 kg ∗ 1 m/s2 |
| F | Kilogramme-force (kp) | 1 kp = 9,81 N | |
| Travail | E | Joule (J) | 1 J = 1 N ∗ 1 m |
| Puissance | P | Watt (W) | 1 W = 1 J/1 s |
| Courant | I | Ampère (A) | Unité de base |
| Tension | U | Volt (V) | 1 V = 1 W/1 A |
| Flux magnétique | Φ | Weber (Wb) | 1 Wb = 1 V ∗ 1 s |
| Φ | Maxwell (M) | 1 M = 10-8 Wb | |
| Induction magnétique | B | Tesla (T) | 1 T = 1 Wb/ m2 |
| B | Gauss (G) | 1 G = 10-4 T | |
| Force magnétomotrice | MMF | Ampère-tour (At) | 1 AW = 1A ∗ 1 Wdg. |
| Θ | Gilbert (Gb) | 1 Gb = 0,796 AW | |
| Intensité du champ magnétique | H | Ampère-tour/mètre (At/m) | 1 At/m = 1 At/ 1 m |
| H | Oersted (Oe) | 1 Oe = 79,6 At/m | |
| Réluctance | R | Ampère/Weber (A/Wb) | 1 A ∗ Wb-1 = 1 mho/s |
| Résistance électrique | r | Ohm (n) | 1 Ω = 1 V/ 1 A |
| Conductance électrique | G | Siemens (S) | 1 S = 1 Ohm-1 = 1 mho |
Longueur
Heure
Masse
Force
Travail
Puissance
Courant
Tension
Flux magnétique
Induction magnétique
Force magnétomotrice
Intensité du champ magnétique
Réluctance
Résistance électrique
Conductance électrique
Les matériaux magnétiques et leur création
AlNiCo
Les premiers matériaux magnétiques à avoir été utilisés dans l’industrie datent des années 20. Ce type d’aimant se présente sous la forme d’un alliage d’acier coulé en aluminium, nickel, cobalt et fer et est connu sous le nom d’AlNiCo. Initialement, il était fabriqué en Angleterre. L’un des principaux noms de marque était « Eclipse ».
Ferrite dure
Pendant la Seconde Guerre mondiale, l’Allemagne n’a u importer aucun matériau d’alliage pour l’acier. Une nouvelle catégorie de matériaux magnétiques, la ferrite, a donc été inventée au sein du Reich. Ce nouveau matériau a été fabriqué en frittant de l’oxyde de fer (déchet de la sidérurgie) avec du baryum ou du strontium de métaux lourds disponibles. Les fabricants d’aimants établis en Angleterre ont désigné ce matériau sous le terme de « dirty magnets » (aimants sales) car ils considéraient son traitement comme étant salissant. D’un point de vue magnétique, ce nouveau matériau n’était pas une révolution et était de qualité plutôt médiocre. Néanmoins, il a connu son heure de gloire dans les années 50 car il pouvait être fabriqué à un prix nettement inférieur par rapport aux autres matériaux magnétiques.
Plastoferrite et ferrites à liant synthétique
Peu de temps après l’invention de la ferrite dure, un nouveau matériau a vu le jour : l’aimant souple.
Celui-ci est obtenu en incorporant de la poudre d’aimant de ferrite avec un taux de remplissage élevé à une matrice plastique. Les performances en matière de propriétés magnétiques sont réduites d’env. 30 %, mais c’est précisément la raison pour laquelle le matériau est populaire et largement utilisé dans la publicité et les marquages de stock.
Ce matériau s’est également imposé dans la construction de moteurs électriques sous forme de moules d’injection ou de pièces moulées. Ce matériau est conçu comme un plastique thermodurcissable. Il est donc dur et indéformable. Il a permis en particulier de façonner des engrenages ou d’injecter des essieux.
Samarium-Cobalt
Ce matériau a été inventé en Suisse à la fin des années 60. Le samarium cobalt a permis de faire un grand bond en avant en matière de technologie des matériaux, car ce matériau magnétique a permis d’obtenir un rendement magnétique plusieurs fois supérieur à celui de la ferrite dure et de l’AlNiCo. Au cours des dix premières années, ce matériau n’a été utilisé que dans des applications spéciales. Grâce à ses propriétés particulières en matière de comportement thermique, de stabilité magnétique et de résistance à l’oxydation, ce matériau est encore aujourd’hui incontournable dans l’industrie.
Néodyme (super aimants)
De nos jours, le néodyme est le leader incontesté des matériaux magnétiques. Lui aussi doit son succès à son excellent rapport qualité/prix. Cependant, ce matériau présente quelques inconvénients : étant donné que le demi-élément bore est intégré, l’alliage est instable et certaines méthodes délicates sont nécessaires pour rendre les matériaux stables à l’utilisation. Si ses performances n’étaient pas meilleures par rapport à tous les autres matériaux magnétiques et que son prix n’était pas si bas, personne n’utiliserait un alliage aussi instable.
Ce matériau magnétique présente deux inconvénients : la source de ses matières premières et son affinage. 97 % de la prospection mondiale des matières premières a lieu en Chine, de même que plus de 60 % de l’affinage. D’où une dépendance incroyable vis-à-vis des fournisseurs chinois. On ne peut ignorer également la contamination par des sous-produits radioactifs qui survient lors de l’extraction de cette terre rare. Les dommages environnementaux pourraient devenir immenses, comme cela s’est déjà produit en Malaisie voilà quelques années. Autre problème : le matériau magnétique est principalement utilisé pour les jeux et les divertissements. Cela vaut-il vraiment la peine que la Chine exploite ses ressources et les mette sur le marché à bas coût?
La dépendance du monde occidental est si importante que des recherches ont déjà été lancées afin de trouver des alternatives permettant de se passer de ce matériau magnétique. Cela concerne avant tout l’industrie automobile qui utilise des moteurs électriques. Le constructeur automobile américain Tesla a opté dès le départ pour des moteurs asynchrones sans aimant permanent. Les fabricants européens s’appuient pour leur part sur les moteurs synchrones dotés d’aimants permanents.
Plasto-néodyme
Comme la plastoferrite, ce matériau de substitution a vu le jour en tant que matériau magnétique souple dans les années 90. Le plasto-néodyme présente une force d’adhérence dix fois supérieure à celle de la plastoferrite.
Avenir des matériaux magnétiques
Aucune nouvelle génération de matériau magnétique n’est prévue dans un avenir proche. Les recherches portent principalement sur le remplacement des matières premières difficiles à obtenir et sur le recyclage optimal des matériaux magnétiques. Malheureusement, les terres rares fortement oxydantes sont difficiles à isoler en vue de leur recyclage. L’accent doit donc être mis sur la réutilisabilité des aimants. Jusqu’à présent, cette approche n’a réussi que dans le cas des gros générateurs d’éoliennes. Dans ce domaine, de gros segments magnétiques sont montés au moyen de vissages mécaniques afin que l’aimant puisse être démonté et réutilisé sans être endommagé.
Dans la fabrication additive, un procédé par injection à froid est en cours de développement. Le Conseil national de recherches Canada (CNRC) espère une résistance plus élevée et des options de construction plus complexes par rapport aux terres rares frittées, ainsi que des valeurs magnétiques satisfaisantes et une résistance à la corrosion plus élevée. En outre, les structures de système associées à des culasses polaires en fer n’ont plus besoin d’être assemblées ou collées.
Disponibilité et développement des matériaux magnétiques
Les principaux groupes de matériaux magnétiques sont subdivisés en un certain nombre de variétés secondaires.
Ces segments reflètent principalement les étapes de développement des différentes options de fabrication. Les propriétés visent principalement à générer des produits d’énergie plus élevés (BHmax) et à augmenter la rémanence (Br) et la force coercitive (Hcj). La teneur énergétique et l’augmentation de la rémanence visent à augmenter les performances. Dans le cas de la force coercitive (force de résistance), l’objectif consiste à améliorer ou à augmenter la température de fonctionnement et la démagnétisation sectorielle des aimants dans les moteurs électriques, également appelée empreinte.
Propriétés magnétiques
AlNiCo
Les aimants AlNiCo se caractérisent en particulier par les propriétés suivantes:
- Stabilité thermique de 0,02 % par °C
Les aimants AlNiCo conviennent donc parfaitement lorsqu’il s’agit de stabiliser la température dans les systèmes de pesage et les applications de capteurs. - Température de service élevée jusqu’à 500°C
Dans certains cas, des températures dépassant le seuil de la classe de matériaux la plus proche (SmCo à 350°C) sont atteintes. L’AlNiCo est le seul matériau pouvant être utilisé dans ces cas, par exemple, pour les supports des processus d’enduction PVD. - Stabilité magnétique
La magnétisation affiche une grande stabilité, mais la condition préalable est une démagnétisation de stabilisation. Ce matériau est très sensible aux champs externes, ce qui nécessite la plus grande attention.
Ferrite dure
La ferrite présente les propriétés suivantes:
- Courbe de températures la plus élevée de tous les matériaux avec 0,2 % par °C
- Faible température de service, plage de -20°C à 220°C
- Faible produit énergétique, faibles performances
- Poids élevé par rapport aux performances
- Résistance à l’oxydation
- Isolation électrique, 105 Ohm/m
- Facilité de magnétisation, 1 Tesla d’intensité de champ de magnétisation
- Prix avantageux
Samarium-Cobalt
Parmi les matériaux, il fait office de solutionneur de problèmes : il convient aux applications délicates de toutes sortes et allie à peu près tous les avantages de toutes les classes de matériaux. Mais attention : il existe en deux classes principales, à savoir Sm1Co5 et Sm2Co17. Le 2:17 présente une rémanence plus élevée et il est moins cher. Contrairement au 1:5, il nécessite une intensité de champ magnétique très élevée (plus de 5 Tesla contre 2,5 Tesla pour le 1:5). Le 2:17 s’oxyde dans l’azote liquide.
L’aimant en samarium cobalt présente les propriétés suivantes:
- résistance thermique élevée, de -273,15 °C (zéro absolu) à 350 °C
- Petite courbe de températures, 0,035 % par °C
- Stabilité magnétique maximale
- Résistance à l’oxydation
- Faibles tolérances de dimensions possibles
- Fragilité du matériau
- Intensités élevées des champs de magnétisation jusqu’à 5,5 Tesla (2:17)
Néodyme-Fer-Bore
Le matériau le plus utilisé, rapport qualité/prix incomparable. Il existe de nombreuses sous-catégories et étant donné que la ces aimants sont presque exclusivement fabriqués en Chine, il est d’usage désormais d’utiliser cette région comme désignation des matériaux. Les classes de performances sont indiquées dans les anciennes unités du système centimètre-gramme-seconde (MGOe – Mega-Gauss-Oersted), ce qui désigne le produit énergétique maximal. En outre, l’indication de la force coercitive a augmenté empiriquement et le comportement thermique n’a cessé d’augmenter avec le développement du matériau.
L’aimant en néodyme présente les propriétés suivantes:
- résistance thermique satisfaisante, de -196°C (azote liquide) à 240°C
- Courbe de températures moyenne, 0,1 – 0,12 % par °C
- Stabilité magnétique satisfaisante
- Très sujet à l’oxydation
- Inconvénient : revêtement nécessaire
- Tolérances de dimensions seulement convenables en raison du revêtement
- Intensités de champs de magnétisation à partir de 1,5 Tesla (matériau spécial), en général, 2,5 Tesla
Des termes quantitatifs sont utilisés pour l’expression visuelle des Chinois.
Les désignations se composent de trois éléments:
La première lettre correspond au matériau, autrement dit, N pour le néodyme.
Divers fournisseurs utilisent leurs propres désignations, ce qui segmente le marché, par exemple, BMN, GSN, REFeB, VACODYM etc. à la base, il s’agit cependant des mêmes matériaux.
Le nombre correspond au produit énergétique, par exemple, 35 pour BHmax. en MGOe.
La lettre correspond à la force coercitive ou à la température : H pour 120°C.
Version tabulaire comportant un récapitulatif d’exemples:
| Teneur en énergie | Température | Température de service | Expression de la température |
|---|---|---|---|
| 35 | 80 °C | Standard | |
| 38 | M | 95 °C | Medium |
| 40 | H | 110 °C | High |
| 42 | SH | 150 °C | Super-High |
| 38 | UH | 180 °C | Ultra-High |
| 35 | EH | 200 °C | Extremely-High |
La suite respecte l’ordre alphabétique:
30 AH 220 °C
25 BH 240°C
Les propriétés d’oxydation doivent être prises en compte. Il existe de grosses différences en la matière, même si de gros progrès ont eu lieu récemment et que les alliages les plus problématiques ont été éliminés. Le test HAST (Highly Accelerated Test) permet d’évaluer le comportement d’oxydation. Il consiste simplement à placer le matériau magnétique sans revêtement dans un autocuiseur. Le matériau y est exposé à une pression de vapeur atmosphérique d’env. 2,6 bar pendant une durée donnée. L’oxydation générée est éliminée et le poids est mesuré.
Au départ, ce test était un test d’humidité intensifié et accéléré. Il permet d’évaluer très rapidement l’effet néfaste de la chaleur humide sur les sujets testés (principalement des composants électrotechniques, fermés de manière non hermétique).
Oxydation après «HAST»

« Highly Accelerated Stress Test » 130°C/95 % d’humidité et 2,6 bar de pression
Le matériau magnétique en néodyme « standard » conventionnel présente les valeurs de déperdition suivantes : 10 mg/cm2 en 6 jours et 100 mg/cm2 en 10 jours.
La société Maurer Magnetic fournit par défaut une qualité de 2 mg/cm2 en 7 jours.
Actuellement, les meilleures propriétés s’élèvent à 2 mg/cm2 en 20 jours. Cela correspond à la série L pour « low weight loss » et à la série L-T pour « low weight loss » et « low temperature coefficient ». Ces séries sont disponibles à partir d’une taille de lot d’env. 300 kg.

Généralement, les aimants en néodyme sont dotés d’un revêtement galvanique ou organique. Les différents revêtements sont adaptés à différents besoins. Les revêtements proposés sont principalement en nickel. Ce revêtement est devenu particulièrement populaire du fait que l’esthétique d’un aimant doit être satisfaisante. Les fabricants chinois le nomment « shiny magnet ». Au départ, un revêtement brillant était synonyme de bonne qualité. Le revêtement au nickel offre une bonne protection. En revanche, il ne convient pas particulièrement au collage. Une couche supplémentaire d’étain ou un revêtement époxy est préférable. Les revêtements au zinc sont également recommandés et font déjà référence.
La société Maurer Magnetic utilise différents revêtements pour différencier les aimants en néodyme proposés dans la gamme standard. Des dimensions similaires sont disponibles en stock pour les matériaux N35, N48 et N45SH. Le N35 présente un revêtement en zinc, le N48, en nickel et le N45SH, en étain en plus du nickel.
Cependant, la majorité des livraisons destinées à l’industrie sont propres au client : il décide donc du matériau, de la forme, du revêtement, de la magnétisation, de l’emballage, etc.